  Page 3.
|
 |
Measurements of body figures and fashion design of clothes. Information about measurements of somatic shapes and proportions of human bodies can be meant in modeling agencies, and also wear designers can consider measuring tools of golden section, as fashion design of clothes and stylish way of life in fashionable magazines and catalogues of garments should be focused on correct proportional ratio of body figures. |
-
Artistic and architectural creativity or fashion design mean use of
proportional sizes for planning art compositions and architectural projects or
stylish clothes, as any art works should possess harmonious mathematical ratios.
Therefore artists and architects, and also fashion designers can calculate
correct and beautiful mathematical ratios in works of fine arts or architectural
plans, or wear products according to proportions of golden section which is the
key principle of global harmony.
The most obvious proportions of golden section are in linear ratio of pentagon,
but also geometrical figures of other correct polygons possess proportional and
harmonious ratios of lines, and in particular harmony of proportions exists in
the linear network of heptagon. Therefore for calculations of proportional sizes
in the fine arts and architecture, and also in the fashion industry it is
possible to use the diheptagonal geometrical network in which lines of two
heptagons are connected. Namely proportional sizes and mathematical ratios of
art compositions or architectural projects, or models of female dresses and
man's wear can be calculated by means of measuring tools which are constructed
according to lines of diheptagonal geometrical network. That is possible to see
in charts which show multi-colored set-squares or "angle-rulers" which are
constructed according to lines of diheptagon and are universal measuring tools
for calculations of mathematical proportions in a context of the fine arts and
architecture, or in a fashion design of clothes.
The shown set-squares are constructed in the geometrical network of lines which
are entered within the correct circle, and the alive circle is not
used as mathematical ratio of alive figures are very complex and in essence
are not required for decisions of simple art tasks.
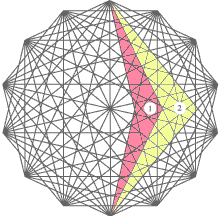
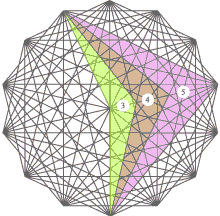
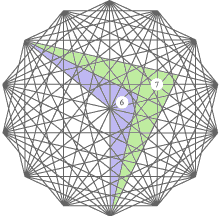
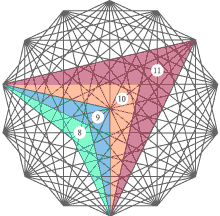
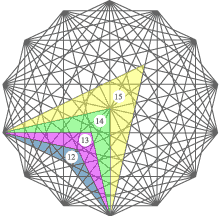
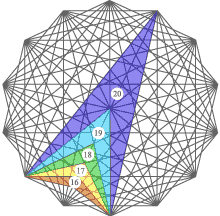
Charts show twenty set-squares which are sufficient to construct any architectural drawings or art pictures, or fashion designs. For example, by means of the first set-square it is possible to measure size of human height or stature, and the fourth set-square allows to measure size of a head, as shown in the following chart.
 |
For drawing a human body it is necessary to scale
diheptagonal geometrical network of lines according to the sizes of
prospective art images or architectural plans, or wear drafts, then it
is necessary to isolate necessary set-squares from a geometrical
network, and then it is possible to do measurements. Namely set-squares should be measuring tools which are scaled according to the demanded sizes of a picture or drawing, or any other sketch. In particular measuring tools of the shown set-squares are necessary for scaling according to the sizes of a human body if art task is the image of a woman. |
-
Construction of correct proportions of human bodies is a complex problem of
the fine arts or design of clothes, but any shapes and parts of a body can be
calculated by means of shown set-squares, and also it is possible to calculate
poses of somatic parts and shapes in space. Namely it is possible to calculate
poses of hands and legs, or various positions of a head, and in all cases
mathematical ratios of body shapes in space of art works will be proportional
and harmonious, as drawings or pictures will correspond to proportions of the
diheptagonal network of lines.
Actually lines of the diheptagonal geometrical figure correspond to mathematical
proportions of ideal patterns of male and female human bodies and harmonious
ratios of golden section, and consequently this polygon allow to measure ideal
sizes in architectural projects and art compositions, or in style clothing of a
fashion design.
It is possible to assume that the golden section is derivative from
heptagonal and diheptagonal linear crossings in the event that these geometrical
figures are entered in space of alive circle. And if the circle is correct then
proportions of these polygons do not coincide with numerical values of golden
section a little, that demands more detailed scientific researches. But however
heptagon and diheptagon have geometrical proportions which allow to draw images
of ideal human bodies.
Besides from geometrical linear crossings of diheptagonal network it is
possible to isolate other figures which too can be used as measuring tools in
the fine arts and fashion design. For example, it is possible to take
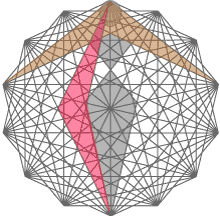
"incongruent set-squares" which are shown in the following chart.
|
Incongruent set-squares have unequal sizes of legs or wings. Functionalities of such measuring tools consist that for calculation of proportional sizes it is possible to use any one incongruent set-square when for calculation of the same sizes it is necessary to use two and sometimes three congruent set-squares. And also functionalities of incongruent set-squares allow to calculate spatial perspectives of drawings or pictures, or other art space. For example, the art problem consists that it is necessary to plant a tree in landscape of a garden or park. For this purpose it is possible to take any incongruent set-square and to scale it concerning sizes on architectural plan of a garden, then it is possible to connect legs of set-square with any objects available in a landscape, and then to find a place for landing a tree in the basis or top of measuring tool. Namely incongruent set-squares have the long leg X, the short leg Y, the top O and the basis Z, that is shown in the following chart. Hence, it is possible to connect legs with other trees in a garden and to plant a new tree in points Z or O, and as a result positions of trees in landscape will correspond to proportions of lines in a heptagon. Similarly landscape designers can measure and calculate arrangements of stones in Japanese rock gardens according to lines of the diheptagonal geometrical figure by means of measuring tools of set-squares. About what look the information on pages of this website in other section with the name: garden of stones. |
-
Various set-squares can be considered as sets of geometrical pieces by means
of which it is possible to make logic puzzles or conundrums. And accordingly
various architectural and art problems, or tasks of fashion design and gardening
can be considered as logic puzzles if artists and architects, or landscape
designers solve problems by means of measuring tools of shown set-squares.
In particular planting of trees or arrangement of stones in landscapes of
Japanese rock gardens can be perceived as geometrical problem of a logic puzzle
which decision is rather entertaining action if the task is for decision by
means of set-squares.
More detailed information about logic games and puzzles by means of pieces of
geometrical figures within the limits of heptagon look on the fourth page in
this section of website.
Besides set-squares of the diheptagonal geometrical linear network can be used
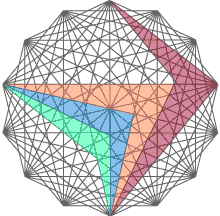
as incongruent compasses, that is shown in the following chart.
 |
The shown figure is incongruent compasses which
consists of two set-squares which are connected in tops by means of a hinge. Two set-squares can move relative each other, and the point of relative movement are tops where there is a hinge. The chart shows one proportional compasses which is an example, but similarly it is possible to isolate other necessary measuring tools from lines of the diheptagonal geometrical network. |
Incongruent compasses allow to measure and calculate sizes which can be
scaled during calculations. Namely set-squares should be preliminary scaled in
sizes of art images and architectural projects, or drafts of fashion designs and
plans of landscape gardening, but by means of incongruent compasses it is
possible to scale proportions of sizes during calculations.
For example, there is some magnitude XY for which it is necessary to calculate
proportional size of magnitude X1Y1.
For this purpose it is necessary to correlate legs of incongruent compasses
with magnitude XY, and as a result we shall receive proportional magnitude
X1Y1
which corresponds to distance between adjacent legs.
I can not result more examples for use of the shown measuring tools in a
context of the fine arts and architecture, or in the fashion industry and
landscape design, as any art problem consists in the unique decision of this problem.
There are no identical problems and consequently each decision is an act of
creativity as a result of which every possible geometrical decisions can be found.
Actually set-squares and incongruent compasses are universal measuring tools
which allow to solve various geometrical problems not only in the fine arts, but
also in different spheres of a human life. In particular in the field of a
fashion and design of clothes, or in any other projects of designing. And also
in a context of plastic surgery for measurements of proportions in a human face and body.
Compasses and set-squares are sacral symbols which symbolize global harmony and
"tools of world creation". On some Christian icons it is possible to see images
of set-squares which symbolize wings of cherubs. And also a set-square with
compasses form the emblem of masons, as these tools of proportional measurements
are attributes of builders and architects.
The following page results some geometrical puzzles and conundrums which can be made of set-squares in linear polygonal geometrical networks.
