|
1. Лингвистическая головоломка или лабиринт линий.
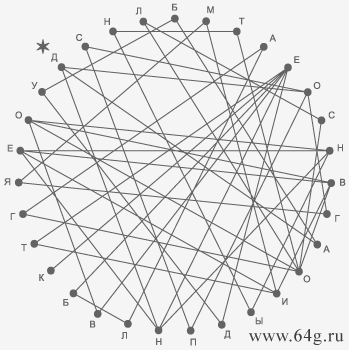
2. Головоломка языка или геометрический лабиринт письменности.
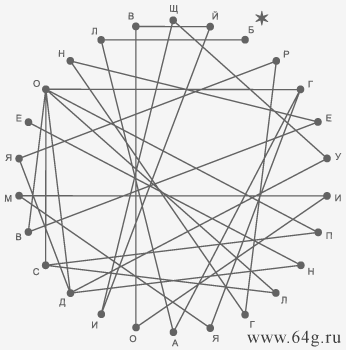
3. Геометрический шифр человеческой речи или код языка.
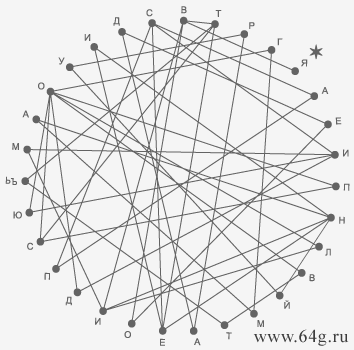
4. Головоломка букв или лингвистический лабиринт.
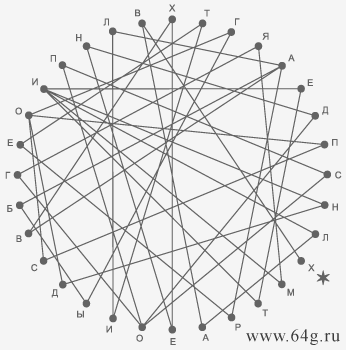
Ответы головоломок.
1. Псалом 112 стих 2 в Библии.
2. Псалом 117 стих 26 в Библии.
3. Псалом 84 стих 8 в Библии.
4. Псалом 134 стих 1 в Библии.
|
Законы геометрической лингвистики.
Лингвистические лабиринты букв.
Показанные геометрические шифры по существу являются лингвистическими лабиринтами,
в которых линии обозначают
последовательность букв в словах и образуют смысловое семантическое содержание,
или можно сказать, что линии обозначают путь лабиринта, в котором зашифрованы слова.
Каждый лабиринт - это множество узловых точек, которые
сопоставлены с буквами алфавита. А также каждый лабиринт - это множество
линий, которые соединяют узловые точки и указывают переходы между
буквами, что образует путь, который должен быть пройден, и в
результате буквы должны образовать последовательность слов.
Заглавная буква геометрического шифра в начальной точке лабиринта
указана специальным символом, который необходим, поскольку при
отсутствии указания первая буква каждого слова может восприниматься как
начало лабиринта, то есть каждое слово может быть воспринято как начало
фразы, которая закодирована в шифре.
Если шифр содержит одно слово, то начальная буква может быть не обозначена.
Конечная точка лабиринта специально не обозначена,
то есть последовательность слов в шифре имеет неопределённое окончание.
Если в точку лабиринта есть вход (входящая линия), но нет выхода
(исходящей линии), то очевидно, что это последняя буква шифра.
Если последняя буква находится в точке, где соединены
несколько линий, то есть у точки лабиринта есть вход и есть возможный выход,
то окончание зашифрованной фразы является неопределённым.
Каждая точка может быть пройдена несколько раз, то есть буквы могут повторяться, и в результате путь
лабиринта может проходить одни и те же точки многократно.
Каждая линия тоже может быть пройдена несколько раз, то есть путь лабиринта может
пролегать по ранее пройденным линиям. Но имеет силу правило, согласно
которому нельзя выйти из точки лабиринта по линии, по которой совершён вход.
Последовательности слов в шифрах не имеют каких-либо иных символов кроме
букв алфавита, то есть знаки препинания и промежутки между словами
являются неопределёнными. В связи с этим зашифрованные фразы могут иметь
неоднозначные смыслы, но в контексте геометрической лингвистики это
является интегральным принципом или иначе сказать необходимым правилом,
а также фактором и условием, согласно которому шифры и
коды слов можно рассматривать как интеллектуальные загадки или логические головоломки.
Например, пресловутая фраза "казнить нельзя помиловать" обладает
двойным смыслом, но согласно правилам геометрической лингвистики во
внимание принимаются оба альтернативных значения, а по существу
допускается неопределённое расположение запятой.
А именно в контексте геометрической лингвистики зашифрованные фразы могут состоять из нескольких
мыслей или последовательных высказываний, которые обычно разделены союзами или знаками
препинания, но если знаки препинания отсутствуют, то фраза
распадается на отдельные, но всё же зависимые друг от друга высказывания.
Поэтому необходимо иметь в виду, что в пределах шифра в линиях
лингвистического лабиринта может быть
несколько завершённых высказываний или промежуточных смысловых окончаний, но после каждого смыслового
окончания может следовать продолжение фразы. Например, фраза
"взошло солнце, открылся свет и стало утро" имеет промежуточные
смысловые окончания после слов СОЛНЦЕ и СВЕТ, что может быть
причиной неправильного решения головоломки и ложного завершения пути в
лабиринте, и в результате дешифрация будет незавершённой. На следующей странице
также приведены изображения геометрических шифров, которые можно
рассматривать как интеллектуальные загадки и логические головоломки, или
иначе сказать лингвистические лабиринты букв. А также приведена дальнейшая информация
о правилах языка в контексте геометрической лингвистики.
А также в этом разделе смотрите сведения про шифрование информации в
интернете и законы геометрии человеческой речи, перспективы пространства
в картинах и графических рисунках, символы литературных персонажей и
соотношения имён с наименованиями городов. |