drawings and measurements of a Japanese garden

central page of geometrical plan

space of external continuation of interior
seven points of contemplation in heptagon
reference points of time as stones of Stonehenge
rules for movement of stones in games
dominoes combinations of figures in rules of stones
letters in borders of Japanese garden
stones with philosophical sense

Page 8.

round stone spheres in China and New Zealand

 Japanese garden of stones and methods of measurements  

The eighth page results drawings and methods of geometrical measurements according to which it is possible to draw a heptagonal network of lines and to arrange stones of a Japanese garden on place.

The geometrical plan of a Japanese garden of stones.
Drawings and measurements for an arrangement on place.

When philosophical concepts of a Japanese garden of stones are determined, namely stones are compared to those or other philosophical values, and the person has chosen positions according to which stones will are located in borders of a garden. Then it is necessary to transfer a plan or a preliminary sketch on place where the garden will be located, namely it is necessary to draw a heptagonal network of lines and to arrange stones on a surface of the ground that demands reflection and geometrical measurements which are shown on the chart:

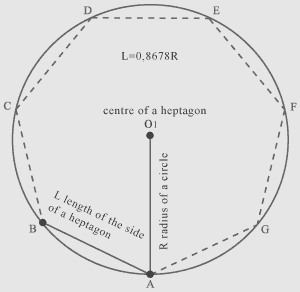to draw a heptagon of lines and to arrange stones of a Japanese garden First, it is necessary to coordinate the sketch to the plan of place and to find the centre of available space where there will be a centre of a heptagon. Then by means of a peg and a cord it is necessary to draw a circle in which the heptagon will be entered:
- establish a peg in centre O1 of a prospective heptagon (in the centre of available space) and fix on a peg one end of a cord;
- determine length of a cord which should be equal to radius R of a circle;
- draw a circle by means of circular movement of a tense cord around of a peg.
Then it is necessary to calculate L length of the side of a heptagon which will be entered in a circle, namely it is necessary to measure length of a cord, and in essence to measure R radius of a circle and to multiply by 0,8678 that in result will give L length of the side of a heptagon, namely L=0,8678R.

Then again by means of pegs and a cord it is necessary to draw a heptagon:
- establish a peg in point A and fix on a peg one end of a cord which has length L;
- pull a cord and combine the second end with a circle and by that find point B;
- establish a new peg in point B and so on find other apexes of a heptagon.
Then connect the found apexes by means of lines and as a result draw a heptagonal network of lines within the framework of which it is possible to have a Japanese garden of stones.
If the available space is limited and it is supposed that borders of a Japanese garden will occupy only a part of a heptagonal network of lines, and in essence it is impossible to find all apexes of a heptagon in available space, then enough to draw a segment of a circle and to find four apexes concerning which it is possible to find projections of other apexes, as shown in the following charts:

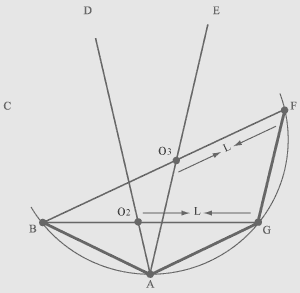plan of apexes of a heptagon and the Japanese garden of stones If four tops of heptagon A B F G are known then it is possible to draw lines FB and GB.
Then establish a peg in point G and attach to a peg one end of a cord which has length L. Pull a cord on line GB and as a result the second end of a cord will specify point O2 where lines GB and AD are crossed, that allows to draw a projection of line AD.
Then establish a peg in point F and by means of a cord having length L similarly find point O3 where lines FB and AE are crossed, that allows to draw a projection of line AE.
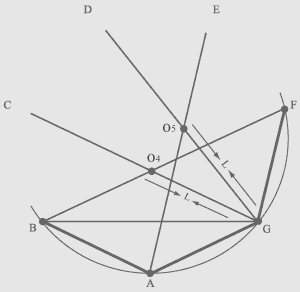borders of a Japanese garden of stones in a heptagon of geometrical lines Then find point O4 by means of a cord attached to a peg in point G and having length L, namely combine the second free end of a cord with line FB that will specify point O4 where lines FB and GC are crossed, and thus draw a projection of line GC.
Then by means of a cord attached to a peg in point G similarly find point O5 where lines AE and GD are crossed, and draw a projection of line GD.
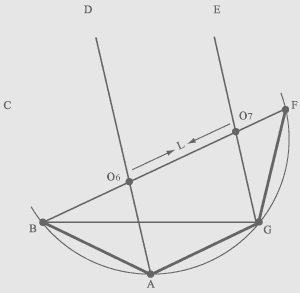geometrical drawings for the Japanese garden of stones on place Then establish a peg in point O6 where lines FB and AD are crossed, and also attach to a peg one end of a cord which has length L. Pull a cord on line FB and as a result the second end of a cord will specify point O7 where lines FB and GE are crossed, that allows to draw a projection of line GE.
And also by means of pegs and a cord having length L find other points of crossings and draw a heptagonal network of lines which is necessary for arrangements of stones in a Japanese garden.

In a similar way, according to four known apexes of a heptagon, the Japanese garden of stones in the temple Ryoanji was constructed, but also by means of pegs and a cord it is possible to draw a heptagonal network of lines in the event that three apexes of a heptagon are known only, and it is actually possible to construct a garden of stones of any configuration.

The following page describes points of a Japanese garden of stones and a heptagonal network of lines where the observer can be.

previous - upwards - following